こんにちは、WaTTsonです。freee Developers Advent Calendar 2025 の12月19日(金)の記事は、freee 技術の日 2025で披露した折紙についてお話しします。
2025年11月30日に行われた自社カンファレンス「freee 技術の日 2025」では、TAMARIBAステージの『使いやすい基盤マイクロサービスを作るための現状分析と対策』という発表を、テックリードのshallowさんと一緒にやりました。
こちらもぜひ見てほしいのですが、この「freee 技術の日 2025」で私が関わったコンテンツとしては、もう一つ大きなものがあります。
それは「おりがみ」です。

「freee 技術の日」は今年で3回目になりますが、毎年それぞれ何かしら、遊び心のあるコンテンツを提供しています。第1回は「書道」、第2回は「ぬりえ」だったのですが、今年の第3回は「おりがみ」をすることになりました。
公式サイトの「おりがみ」のところにあるイラストは、伝承の「ツバメ」の作品なのですが、せっかくならオリジナルな作品を作ろう、ということになりました。私は小学生の時から日本折紙学会(JOAS)に関わっており、機関誌『折紙探偵団』を読んだりコンベンションに参加したりして、折紙作品の創作についてちょっと心得があったので、これを生かせると良さそう、という話になりました。
創作でどのようなものを作るかは、色々な候補が挙がったのですが、ここではfreeeの公式キャラクター「Sweee」を作ることにしました。Sweeeは2024年の4月に誕生したキャラクターで、技術の日では着ぐるみのグリーティングなども行われていたものです。

これを元に、実際に創作した折紙作品はこちらです:

当日使用した折り図をPDFで公開しているので、良かったらぜひ挑戦してみてください:
この記事では、この折紙作品「Sweee」がどのようにしてできたのかを解説します。
円分子法
現代の折紙作品の創作には、色々な理論が知られています。その中で、最も汎用的でよく使われているものが「円分子法」というものです。今回の「Sweee」も大雑把にはこの円分子法を使って創作したので、まずはこれについての説明をしたいと思います。
折紙で複雑な造形を作る時、難しいのは「カド」を折り出すことです。平面の紙から「カド」を折るには、どういう風にすれば良いでしょうか?これは、抽象化して考えると、下図のようになります。
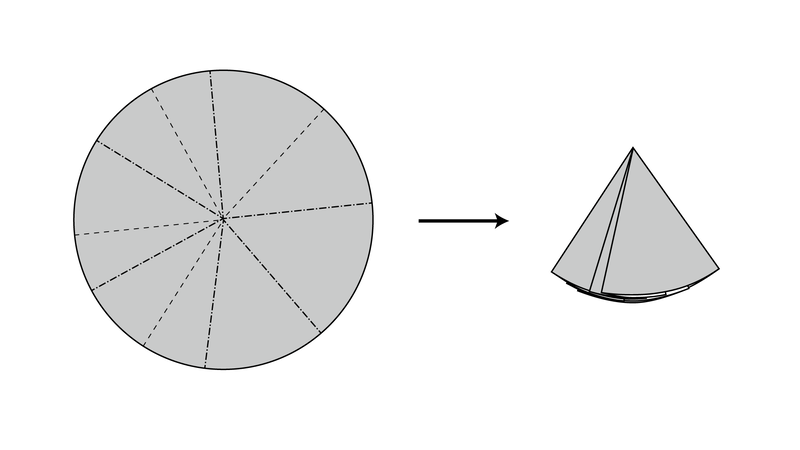
一定の長さのカドを平面の紙の中から折り出すには、そのカドの長さ分の半径を持った円形の領域が必要、ということになります。そこで、必要な長さのカドを必要な数だけ折り出すには、円形の領域を紙の上にうまく配置すれば良い、という発想が生まれます。この原理を用いた折紙の設計技法が「円分子法」と呼ばれるものです。
簡単な例で見てみます。例えばこれは伝承の「折り鶴」(の途中に出てくる"鶴の基本形")の展開図です。
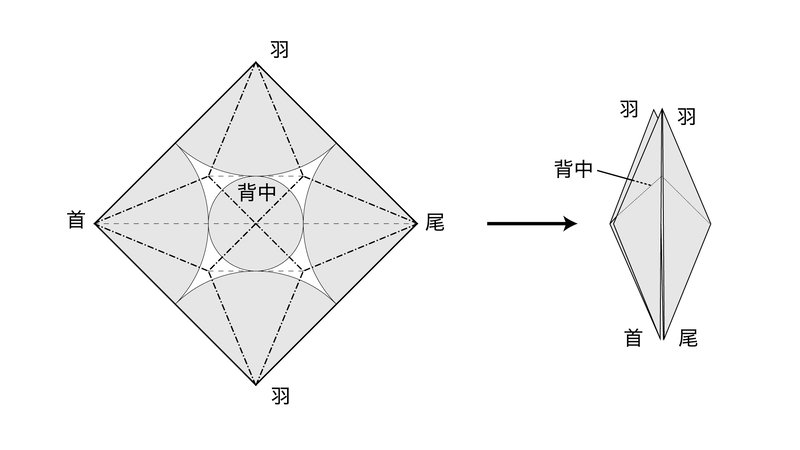
折り鶴は、「首」、「尾」、「羽」×2 の計4つの大きなカドがあり、背中の部分に小さなカドがある構造になっています。"鶴の基本形"では、大きなカド4つを正方形の紙の四隅に配置する形でこれを作り出しています。なお、円分子法でカド折り出しに用いる円は、紙の端に配置される場合には半円や扇形の形になります。
Sweeeのカド配置
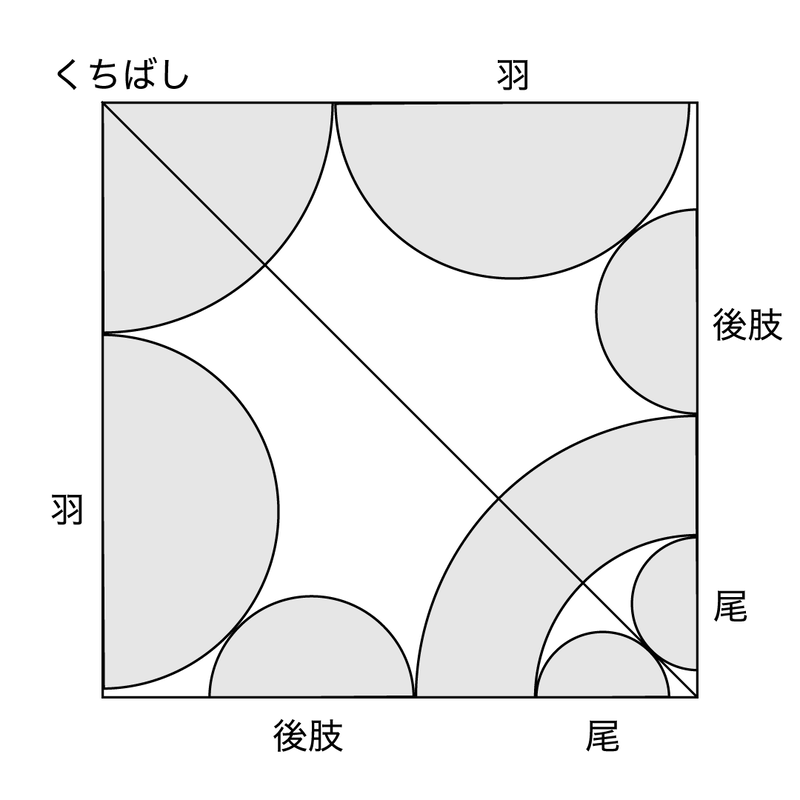
この「円分子法」を使ってSweeeの設計を行います。Sweeeに必要なカドは、「くちばし」、「羽」×2、「足」×2、「尻尾」で、さらに尻尾の先は二つのカドに分かれるようにしたいです。Sweeeはツバメなので、二股に分かれた尻尾は是非とも実現したいです。
円分子法では、二股に分かれるようなカドは円と帯の組み合わせで表現できることが知られています。
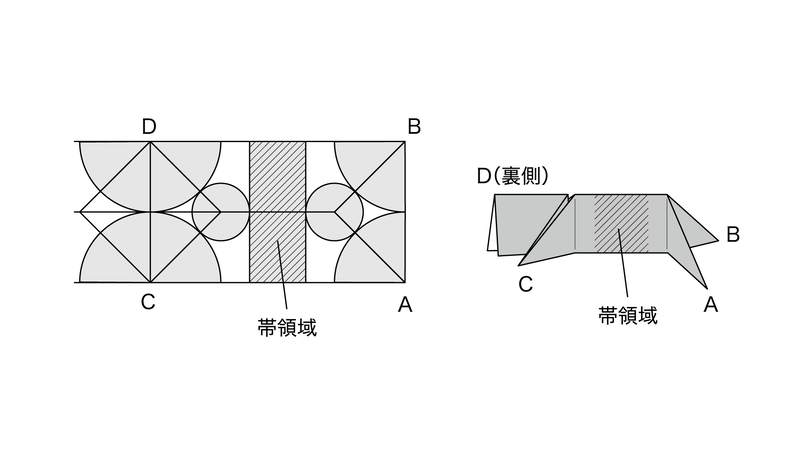
尻尾の部分はこれに似た形になることを考え、ざっくりカドの長さを想像しながら適当に円を置いていくと、例えばこのような形になります。
折紙分子
さて、ここまで円分子法の「円」の部分について説明をしましたが、もう一つ重要な要素として「分子」の概念があります。これは、折紙の展開図上でひとまとまりになっている多角形の組み合わせのことです。折り鶴(鶴の基本形)の展開図の場合、4つの直角二等辺三角形の分子から構成されています。
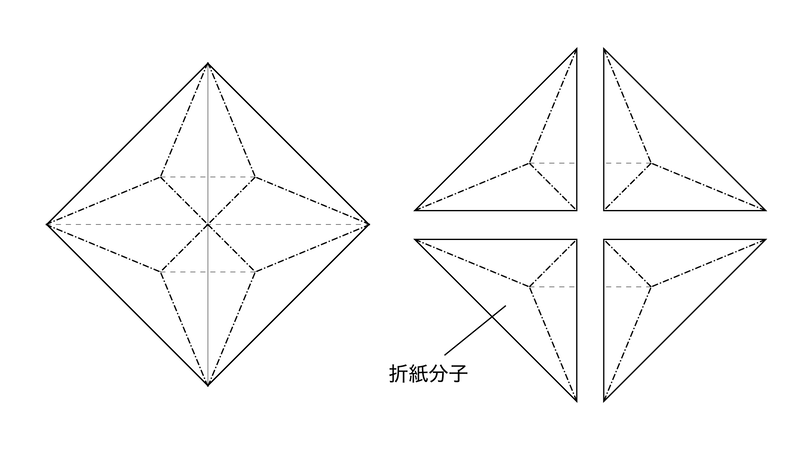
紙の上でカド配置を決めたら、その間の線を結んで適当に多角形(おもに三角形)分割をし、分割した領域内に折紙分子を当てはめるようにすれば、円領域で配置したカドを持つ基本形を折り出すことができるようになります。
インサイドアウト
Sweeeの場合は、カド折り出しの要素に加えてもう一つ、別の種類の工夫も行いました。それは、表裏の紙の色を使い分けることで模様を表現する「インサイドアウト」の技法です。Sweeeでは全体が青色で、お腹の部分だけ白色になるようにしたかったので、青と白の折紙を使ったインサイドアウトに挑戦しました。
インサイドアウトの技法は、カドの折り出しと比べるとあまり体系化されていないように思います。ちょっと私は最近の折紙創作情勢にそこまで詳しくないので実は最近はある程度理論化されたものがあるのかもしれないですが、少なくとも私がよく折紙作品の創作を行っていた時期にはインサイドアウトの効果的な創作理論はあまり知られていませんでした。なので、ここは理論的にというよりは感覚でやっています。
Sweeeの場合、インサイドアウトとはいっても青い領域と白い領域がまとまっているので、比較的単純な構造で実現しています。基本的なイメージは下図のような形です:
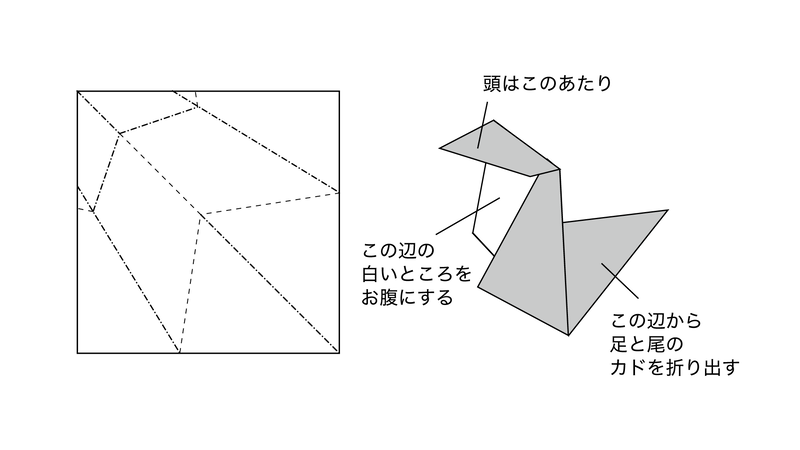
このような折り出しをすることを考えると、紙の中央部分に十分な領域が必要になります。そこで、カド配置を考える時にこれを考慮して円領域のサイズなどを調整しました。
正確な配置を決める
ざっくりカド配置・折紙分子の配置・インサイドアウトの設計を考えると、とりあえずそれをベースに試作品を作ります。この段階では、カド配置は雰囲気で置いているので、細かい部分で折り線に齟齬が出てきます。これを、うまいこと辻褄が合うように調整していきます。
折り図の工程2〜3の手順で、紙を対角線に合わせて斜めに折って付けた位置を基準に長方形の折り筋を付ける、ということをやっていますが、これは各折紙分子のサイズが辻褄が合うようなサイズ比率を幾何学的に計算して付けられているものです。右下の尻尾の部分の紙の縁の長さを1とおいて順に計算していくと、左辺の○印で分けられた上下の長さが と
になります。この2つの比率は
に等しいので、22.5°で折った線の辺との交点として求めることができます。これが折り図の工程2に対応するわけです。
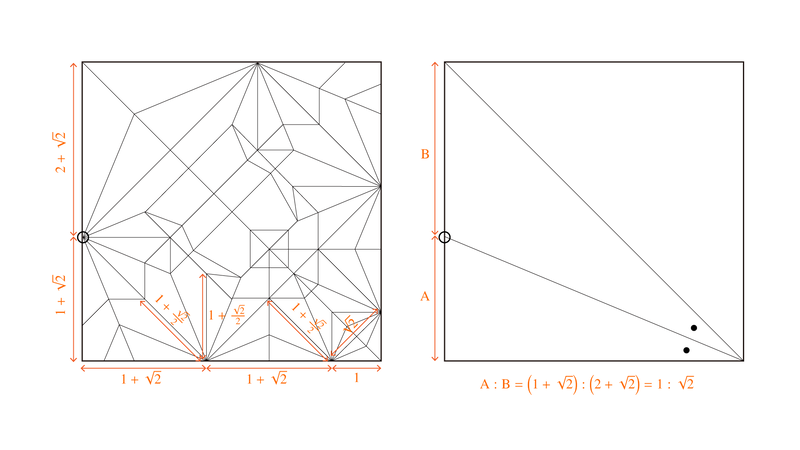
計算がぴったりハマって、うまく折りたためるように決まると結構気持ち良いところがあります。試作品でざっくりした位置関係で作っているとかなりぐちゃぐちゃになるのですが、正確な長さ折り出しをして折ると折りたたんだときに揃うべき部分がきちんと揃う形になって綺麗に折りたためるようになります。個人的に、折紙作品の創作をする時に一番楽しい部分です。
折り図を作る
カド配置が決まったら展開図が確定するので、ある程度複雑系折紙に慣れた人であれば、この展開図だけからもう作品を折れるようになります。展開図は折り図の最後のページに掲載しているので、これだけを見て折ってみる、というのをやってみると面白いかもしれません。展開図の線に沿って折りたたむと、折り図の工程45の形になります。
一般向けに提供する上では、展開図だけ示して折ってもらうのはちょっと大変なので、順番に折っていけるような折り図を作りました。これは、基本的には展開図に付いている線を付ける+その通りに折りたたむ、というのをステップに分けて書くだけです。全ての線を事前に付けるのではなく、折りたたみながら線を付けていくような形でステップを分けるように工夫しています。ただ、工程28の部分をうまく簡単なステップに分解するのができなくて、ここの工程はほぼ展開図の折りたたみのような形になってしまっています。
折り図の図を描くのは、著名な折紙作家である小松英夫さんが2019年に行っていた『Affinity Designerでの折り図制作解説配信(導入と基礎)』という配信のアーカイブを参考にしました。基本的にこれまでは自分で創作した作品は展開図までしか作らないことが多かったので、初めて折り図を作るところまでやったのは面白かったです。図の量が多いのでちょっと大変なんですが、前のステップをコピペしてから修正する、というのを繰り返すことで見かけよりはちょっと楽に作れるというのは学びでした。
感想
きちんとした折紙の作品を作るのはかなり久しぶりだったのですが、良い感じに仕上がって良かったです。特に、インサイドアウトの部分はうまく設計できるか難しい部分だったので、ここが綺麗に収まったのはちょっと嬉しかったです。
ただ、一般向けに提供するものとしてはちょっと難しい作品になってしまった側面はあるかもしれません。私は測ってみたら最短で10分ちょっとくらいで完成まで折れたのですが、事前に社内で講習会をやったときには1時間半くらいかかったり、途中で諦めてしまったりする人も出てしまいました。工程28のような難しめのステップがあることは自覚していましたが、「フチを折り筋と合わせて折り筋を付ける」「点と点を結んで折り筋を付ける」みたいな工程が、慣れていないと結構難しいということに改めて気づかされました。展開図から作品を折るのを繰り返しているとこの辺の感覚が麻痺してくるので、気をつけたいところです。
「freee 技術の日」では、普通のテックカンファレンスとはちょっと変わった、freeeならではのアソビゴコロのあるコンテンツを毎年提供しています。昨年は『CredentialをSlackに書くな高校校歌』の合唱というのをやりました。来年のことはまだ何も決まっていませんが、また何か面白いコンテンツを提供できると良いなと思っています。
freee Developers Advent Calendar 2025の明日の記事の担当は、Reiya Matsumoto (Reiya)さんです。お楽しみに!
